Method – stochasticGW

GW Approximation

Stochastic Resolution of Identity

Stochastic GW Formulation

Fractured Segment Stochastic Resolution of Identity

Reference

GW Approximation

The GW approximation devised by Hedin[1] is a state-of-art method to calculate quasiparticle excitation energies[2][3]:

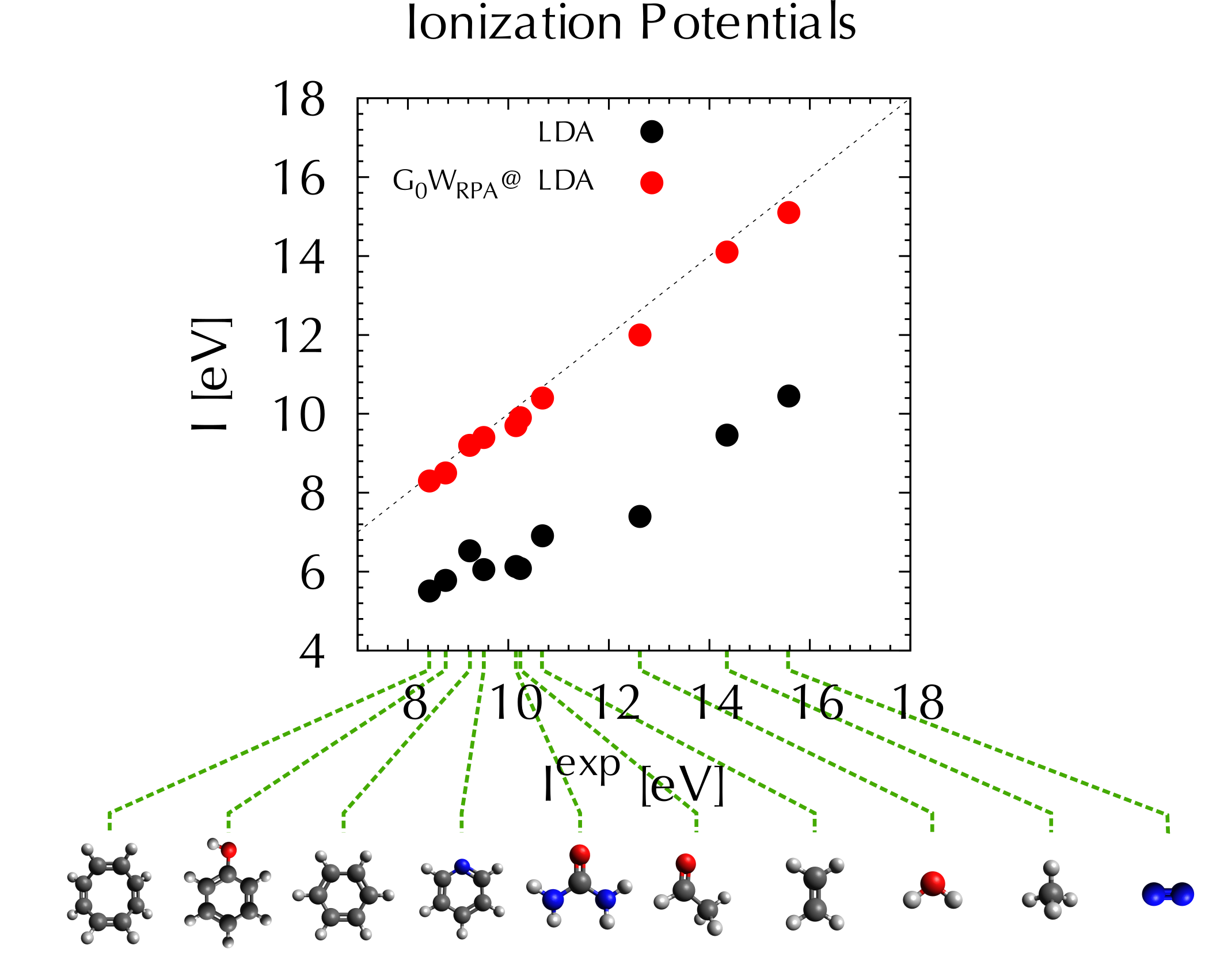
Ionization potentials calculated using LDA-DFT(black dots) and LDA-based one-shot GW(red dots) for some small molecules. The later agrees well with experiment.

$\hat{h}_0(r)\Psi_i(r)+\int d^3r$

The central quantity of interest is the frequency-dependent non-local self-energy operator $\Sigma$ , which includes many-body effects beyond mean field level, and is approximated as a convolution of Green’s function $G$ and the screened Coulomb interaction $W$ :

$\Sigma(r,r$

The original GW was formulated as an iterative method, but often in practice an one-shot calculation is performed. Accuracy of GW quasiparticle energies thus depends on the quality of starting point. LDA-based one-shot GW gives rather satisfactory results for many systems.

The scaling of the usual deterministic GW is quite steep, cubically and usually quartically with system size.

Stochastic Resolution of Identity[4]

Consider numerical wavefunctions defined N discrete spatial grids with volume element $v$ , the identity operator in position basis is given by delta function $\delta(r-r$ . Take a stochastic orbital $|\chi\rangle$ with values $\pm \frac{1}{\sqrt{v}}$ with probability 1/2 independently on each grid point, it follows that:

$\overline{\chi(r)\chi(r$

$=\overline{\chi(r)}\cdot\overline{\chi(r$

$=Cov(\chi(r),\chi(r$

$=\delta(r-r$

Stochastic resolution of identity
As the number of stochastic orbitals increases, the auto-correlation function approaches delta function

Thus, the identity operator is resolved as the auto-correlation of a set of stochastic orbitals:

$\hat{I}=\big\lbrack |\chi\rangle\langle\chi|\big\rbrack_\chi$

Stochastic GW Formulation[5][6]

In time domain, the self energy becomes a simple product of Green’s function and screened potential:

$\Sigma(r,r$

And it could be further separated into the static exchange self-energy and the dynamic polarization self-energy. Evaluation of the latter is the most time-consuming part in GW calculations, which is made very efficient in stochastic GW.

The Green’s function will first be separated using resolution of identity:

$iG_0(r,r$

$=-\langle r|e^{-i\hat{h_0}t}\hat{P}_\mu|r$

$=-\big\lbrack{\langle r|e^{-i\hat{h_0}t}\hat{P}_\mu |\chi\rangle}\langle\chi|r$

$=\big\lbrack{\chi_\mu(r,t)}\chi(r$

where

$\chi_\mu(r,t)=-\langle r|e^{-i\hat{h_0}t}\hat{P}_\mu |\chi\rangle\theta(-t)+\langle r|e^{-i\hat{h_0}t}(\hat{I}-\hat{P}_\mu)|\chi\rangle\theta(t)$

With this breaking up of Green’s function, the polarization self-energy can be written as:

$\Sigma_n^P(t)$

$=\iint\phi_n(r)\phi_i(r$

$={\big\lbrack}\iint \phi_n(r){\chi_\mu(r,t)}{W_P(r,r$

It could be further split by another resolution of identity so that:

$\Sigma_n^P(t)$

$={\big\lbrack}{\big\lbrack}\iiint drdr$

$={\Bigg\lbrack}{\Bigg\lbrack}\Bigg(\int\phi_n(r)\chi_\mu(r,t)\xi(r)dr\Bigg)\Bigg(\iint \xi(r)W_P(r,r$

The first term is a simple integral and easy to obtain, while the second term involves evaluation of the effective polarization potential generated by a fictitious ‘charge density’ $\phi_n(r$ which can be generated using time-dependent Hartree (which is equivalent to RPA) or time-dependent DFT propagation.

In deterministic TDH or TDDFT propagation, all occupied orbitals must be propagated simultaneously, which can be very cumbersome when system size is large. To circumvent this problem, a stochastic version is developed, where another set of stochastic orbitals are projected onto the occupied subspace. Their average density is the true electron density, and typically only a small number of stochastic orbitals will be sufficient. Furthermore, the effort of the stochastic TDDFT is below linear, since as the system size grows fewer stochastic orbitals are needed.

Fractured Segment Stochastic Resolution of Identity[7]

Computational cost can be further reduced if we introduce the fractured segment stochastic resolution of identity (FS-RI). Here instead of generating stochastic orbitals on the full grid, they are generated on only a fraction of the grid points, giving small ‘segments’, each having a fraction span $\alpha$ of the full grid space.